2012年巖土工程師考試基礎知識模擬試題:高等數學(單項選擇題2)
發布時間:2012-07-25 共1頁
高等數學(單項選擇題2)
| 一、單項題的備選項中只有一個最符合題意,錯選、多選均不得分。 |
1.設f(x)是奇函數,且F(x)=f(x)·[1/(a.gif) +1)-1/2]。其中a為不等于1的正常數,則函數F(x)是: +1)-1/2]。其中a為不等于1的正常數,則函數F(x)是: |
| 正確答案:B 解題思路:這是一道概念題,應用奇函數、偶函數的定義,通過代數變形導出最后的結果。 F(-x)=f(-x)[1/(a  +1)-1/2]=-f(x){1/[(1+a +1)-1/2]=-f(x){1/[(1+a.gif) )/a )/a.gif) ]-1/2}=-f(x)[a ]-1/2}=-f(x)[a.gif) /(1+a /(1+a.gif) )-1/2] )-1/2]=-f(x)[2a .gif) -(1+a -(1+a.gif) )]/2(1+a )]/2(1+a.gif) )=-f(x)(a )=-f(x)(a.gif) -1)/2(1+a -1)/2(1+a.gif) ) )=-f(x)(a .gif) +1-2)/2(1+a +1-2)/2(1+a.gif) )=-f(x)[1/2-1/(1+a )=-f(x)[1/2-1/(1+a.gif) )] )]=f(x)[1/(1+a  )-1/2]=F(x) )-1/2]=F(x)F(x)是偶函數。 |
|
|
2.已知冪級數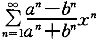 (0<a<b),則所得級數的收斂半徑R等于: (0<a<b),則所得級數的收斂半徑R等于: |
正確答案:D 解題思路:本題考查冪級數收斂半徑的求法。可通過連續兩項系數比的極限得到ρ值,由R=1/ρ得到收斂半徑。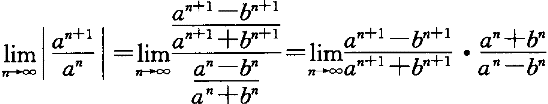 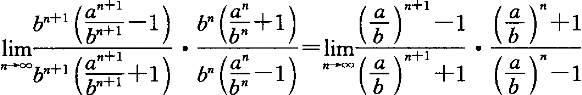 =(-1)/(-1)=1=ρ R=1/ρ=1 |
|
|
3.設二重積分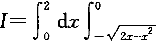 f(x,y)dy,交換積分次序后,則I等于: f(x,y)dy,交換積分次序后,則I等于: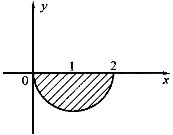 |
| 正確答案:A 解題思路:本題考查二重積分交換積分次序方面的知識。解這類題的基本步驟:首先根據原積分次序畫出積分區域的圖形,得到陰影部分的圖形;然后寫出先x后y的積分表達式。 由 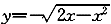 ,y ,y.gif) =2x-x =2x-x.gif) ,x ,x.gif) -2x+y -2x+y.gif) =0,(x-1) =0,(x-1).gif) +y +y.gif) =1。 =1。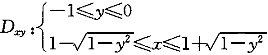 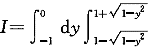 f(x,y)dx f(x,y)dx |
|
|
| 4.下列函數在所給區間中,滿足羅爾定理條件的是: |
| 正確答案:D 解題思路:本題屬于概念題,根據滿足羅爾定理的三個條件(在閉區間連續,在開區間可導,兩端函數值相等)來判定。 A.f(x)=x .gif) 在[0,3]兩端函數值不相等。 在[0,3]兩端函數值不相等。B.f(x)=1/x,f′(x)=-1/x .gif) 在(-1,1)可導的條件不成立,在x=0不可導。 在(-1,1)可導的條件不成立,在x=0不可導。C.f(x)=|x|在x=0處的導數,用左右導數定義計算, 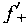 (0)=1, (0)=1,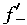 (0)=-1,因而在x=0處不可導,從而在(-1,1)內可導不成立。本題的結論應記住。 (0)=-1,因而在x=0處不可導,從而在(-1,1)內可導不成立。本題的結論應記住。D.f(x)=x  在[0,3]上連續,f′(x)= 在[0,3]上連續,f′(x)=.gif) -x/2 -x/2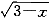 在(0,3)上可導,f(0)=f(3),滿足羅爾定理。 在(0,3)上可導,f(0)=f(3),滿足羅爾定理。 |
|
|
5.求 xf(x xf(x.gif) )·f′(x )·f′(x.gif) )dx等于: )dx等于: |
正確答案:D 解題思路:本題為抽象函數的不定積分。考查不定積分湊微分方法的應用及是否會用不定積分的性質 f′(x)dx=f(x)+c。 f′(x)dx=f(x)+c。 xf(x xf(x.gif) )f′(x )f′(x.gif) )dx= )dx= f′(x f′(x.gif) )f(x )f(x.gif) )d(1/2)x )d(1/2)x.gif) =(1/2) .gif) f′(x f′(x.gif) )?f(x )?f(x.gif) )dx )dx.gif) =(1/2) =(1/2) 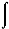 f(x f(x.gif) )df(x )df(x.gif) ) )=(1/2)·(1/2)[f(x .gif) )] )].gif) =(1/4)[f(x =(1/4)[f(x.gif) )] )].gif) +c +c |
- 2012年巖土工程師考試基礎知識模擬試題:工程地質(單項選擇題1)
- 2012年巖土工程師考試基礎知識模擬試題:理論力學(單項選擇題1)
- 2012年巖土工程師考試基礎知識模擬試題:高等數學(單項選擇題3)
- 2012年巖土工程師考試專業知識考前沖刺(五)上午卷
- 2016年巖土工程師考試《綜合知識》沖刺練習(4)
- 2012年巖土工程師考試基礎知識模擬試題:彈性力學和結構力學(單項選擇題2)
- 2016年巖土工程師考試《綜合知識》沖刺練習(3)
- 2012年巖土工程師考試基礎知識模擬試題:電工與電子技術(單項選擇題2)
- 土工結構、邊坡與支擋結構、基坑與地下工程(單項選擇題2)
- 2016年巖土工程師考試《綜合知識》沖刺練習(5)

